說明:上述5例都是根據(jù)題目的自身特點(diǎn),從選擇恰當(dāng)?shù)恼麛?shù)表示形式入手,使問題迎刃而解��。
二�����、枚舉法
枚舉法(也稱為窮舉法)是把討論的對象分成若干種情況(分類)�����,然后對各種情況逐一討論���,最終解決整個(gè)問題��。
運(yùn)用枚舉法有時(shí)要進(jìn)行恰當(dāng)?shù)姆诸���,分類的原則是不重不漏�����。正確的分類有助于暴露問題的本質(zhì)�,降低問題的難度��。數(shù)論中最常用的分類方法有按模的余數(shù)分類�,按奇偶性分類及按數(shù)值的大小分類等����。
例6 求這樣的三位數(shù)�����,它除以11所得的余數(shù)等于它的三個(gè)數(shù)字的平方和�����。
分析與解:三位數(shù)只有900個(gè)��,可用枚舉法解決����,枚舉時(shí)可先估計(jì)有關(guān)量的范圍���,以縮小討論范圍�,減少計(jì)算量���。
設(shè)這個(gè)三位數(shù)的百位�、十位�、個(gè)位的數(shù)字分別為x���,y,z��。由于任何數(shù)除以11所得余數(shù)都不大于10�����,所以
x2+y2+z2≤10����,
從而1≤x≤3,0≤y≤3����,0≤z≤3。所求三位數(shù)必在以下數(shù)中:
100�����,101�����,102�����,103,110�����,111�,112�����,
120���,121�,122�,130,200�,201,202����,
211,212����,220����,221�����,300���,301���,310。
不難驗(yàn)證只有100��,101兩個(gè)數(shù)符合要求���。
例7 將自然數(shù)N接寫在任意一個(gè)自然數(shù)的右面(例如��,將2接寫在35的右面得352)����,如果得到的新數(shù)都能被N整除��,那么N稱為魔術(shù)數(shù)。問:小于2000的自然數(shù)中有多少個(gè)魔術(shù)數(shù)����?
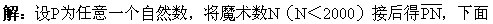
對N為一位數(shù)、兩位數(shù)�、三位數(shù)、四位數(shù)分別討論�����。
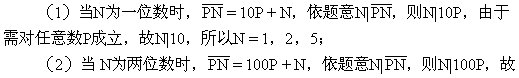
N|100�����,所以N=10���,20,25����,50;
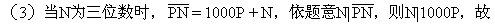
N|1000����,所以N=100��,125�����,200�����,250��,500����;
��。�4)當(dāng)N為四位數(shù)時(shí),同理可得N=1000��,1250����,2000,2500�����,5000。符合條件的有1000�����,1250���。
綜上所述����,魔術(shù)數(shù)的個(gè)數(shù)為14個(gè)���。
說明:(1)我們可以證明:k位魔術(shù)數(shù)一定是10k的約數(shù)����,反之亦然���。
(2)這里將問題分成幾種情況去討論,對每一種情況都增加了一個(gè)前提條件���,從而降低了問題的難度�����,使問題容易解決�����。
例8 有3張撲克牌�,牌面數(shù)字都在10以內(nèi)。把這3張牌洗好后���,分別發(fā)給小明����、小亮��、小光3人�����。每個(gè)人把自己牌的數(shù)字記下后�����,再重新洗牌��、發(fā)牌、記數(shù)��,這樣反復(fù)幾次后����,3人各自記錄的數(shù)字的和順次為13,15��,23���。問:這3張牌的數(shù)字分別是多少�����?
解:13+15+23=51���,51=3×17。
因?yàn)?/FONT>17>13�,摸17次是不可能的,所以摸了 3次���, 3張撲克牌數(shù)字之和是17,可能的情況有下面15種:
������、�1,6��,10 ���、�1���,7����,9 �����、�1,8��,8
�����、�2,5����,10 ����、�2,6��,9 ��、�2,7����,8
⑦3�����,4�,10 ⑧3����,5,9 ⑨3����,6,8
��、�3����,7�����,7 (11)4�,4�,9 (12)4,5�����,8
(13)4��,6�,7 (14)5,5����,7 (15)5,6��,6
只有第⑧種情況可以滿足題目要求���,即
3+5+5=13���;3+3+9=15�����;5+9+9=23�。
這3張牌的數(shù)字分別是3�����,5和9��。
例9 寫出12個(gè)都是合數(shù)的連續(xù)自然數(shù)����。
分析一:在尋找質(zhì)數(shù)的過程中,我們可以看出100以內(nèi)最多可以寫出7個(gè)連續(xù)的合數(shù):90�����,91�,92,93,94�,95,96����。我們把篩選法繼續(xù)運(yùn)用下去�����,把考查的范圍擴(kuò)大一些就行了����。
解法1:用篩選法可以求得在113與127之間共有12個(gè)都是合數(shù)的連續(xù)自然數(shù):
114,115��,116��,117�����,118��,119��,120�,
121��,122���,123,124���,125����,126����。
分析二:如果12個(gè)連續(xù)自然數(shù)中,第1個(gè)是2的倍數(shù)��,第2個(gè)是3的倍數(shù)�,第3個(gè)是4的倍數(shù)……第12個(gè)是13的倍數(shù),那么這12個(gè)數(shù)就都是合數(shù)����。
又m+2,m+3��,…,m+13是12個(gè)連續(xù)整數(shù)�,故只要m是2,3�����,…�����,13的公倍數(shù)�,這12個(gè)連續(xù)整數(shù)就一定都是合數(shù)�。
解法2:設(shè)m為2,3��,4��,…����,13這12個(gè)數(shù)的最小公倍數(shù)。m+2�,m+3,m+4�,…,m+13分別是2的倍數(shù),3的倍數(shù)�����,4的倍數(shù)……13的倍數(shù)��,因此12個(gè)數(shù)都是合數(shù)��。
說明:我們還可以寫出
13���!+2���,13!+3���,…����,13�!+13
(其中n�����!=1×2×3×…×n)這12個(gè)連續(xù)合數(shù)來。
同樣��,
��。�m+1)!+2�����,(m+1)�����!+3����,…���,(m+1)�����!+m+1是m個(gè)連續(xù)的合數(shù)��。
三����、歸納法
當(dāng)我們要解決一個(gè)問題的時(shí)候,可以先分析這個(gè)問題的幾種簡單的�、特殊的情況,從中發(fā)現(xiàn)并歸納出一般規(guī)律或作出某種猜想���,從而找到解決問題的途徑�����。這種從特殊到一般的思維方法稱為歸納法����。
例10 將100以內(nèi)的質(zhì)數(shù)從小到大排成一個(gè)數(shù)字串�����,依次完成以下5項(xiàng)工作叫做一次操作:
����。�1)將左邊第一個(gè)數(shù)碼移到數(shù)字串的最右邊��;
���。�2)從左到右兩位一節(jié)組成若干個(gè)兩位數(shù)���;
�����。�3)劃去這些兩位數(shù)中的合數(shù)���;
�����。�4)所剩的兩位質(zhì)數(shù)中有相同者���,保留左邊的一個(gè)����,其余劃去��;
���。�5)所余的兩位質(zhì)數(shù)保持?jǐn)?shù)碼次序又組成一個(gè)新的數(shù)字串���。
問:經(jīng)過1999次操作,所得的數(shù)字串是什么���?
解:第1次操作得數(shù)字串711131131737�;
第2次操作得數(shù)字串11133173;
第3次操作得數(shù)字串111731��;
第4次操作得數(shù)字串1173�;
第5次操作得數(shù)字串1731;
第6次操作得數(shù)字串7311����;
第7次操作得數(shù)字串3117;
第8次操作得數(shù)字串1173����。
不難看出,后面以4次為周期循環(huán)�,1999=4×499+3,所以第1999次操作所得數(shù)字串與第7次相同����,是3117。
例11 有100張的一摞卡片�,玲玲拿著它們,從最上面的一張開始按如下的順序進(jìn)行操作:把最上面的第一張卡片舍去�,把下一張卡片放在這一摞卡片的最下面。再把原來的第三張卡片舍去�,把下一張卡片放在最下面�。反復(fù)這樣做��,直到手中只剩下一張卡片���,那么剩下的這張卡片是原來那一摞卡片的第幾張���?
分析與解:可以從簡單的不失題目性質(zhì)的問題入手,尋找規(guī)律�����。列表如下:





